- Дисциплина: Математика профильная
- Номер вопроса в билете: 7
- Баллы: 1
- Сложность: Базовый
-
На рисунке изображены график функции y=f(x) и семь точек на оси абcцисс: x1, x2, x3, x4, x5, x6, x7
В скольких из этих точек производная функции f '(x) отрицательна?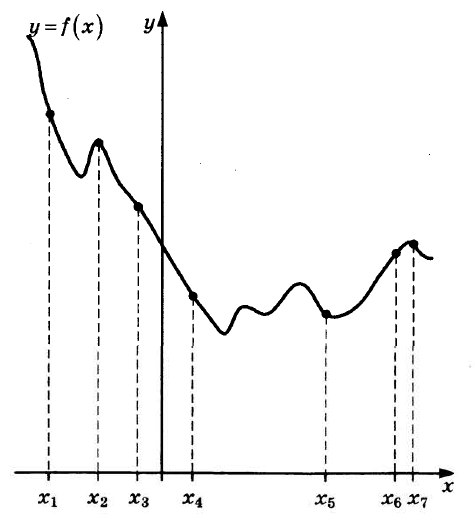
Баллы: 0 - Подробное решение
Есть функция возрастает (каждому большему значению x2 > x1 соответствует большее значение f(x2) > f(x1) или другим словами y2 > y1), график устремлен вверх, то прjизводная положительная f '(x) > 0
Есть функция возрастает (каждому большему значению x2 > x1 соответствует меньшие значение f(x2) < f(x1) или другим словами y2 < y1), график устремлен вниз, то производная положительная f '(x) < 0
если точка - точка максимума (смена с роста на убывание) или минимума (смена с убывания на рост), производная равна нулю f '(x) = 0
x1 - график вниз, производная f '(x) < 0
x2 - очень близко к максимуму, но всё же график вниз f '(x) < 0
x3 - график вниз, производная f '(x) < 0
x4 - график вниз, производная f '(x) < 0
x5 - близка к минимуму, но всё же график вниз, производная f '(x) < 0
x6 - график вверх, производная f '(x) > 0
x7 - очень близко к максимуму, но всё же график вниз f '(x) < 0
У нас получилось 6 точек когда производная меньше нуля.
Рисунок неудачный, особенно трудно понять точка x2 это максимум или участок убывания?
Сайт помог тебе решить задачу?
Помоги нам - задонать!
Помоги нам - задонать!