- Дисциплина: Математика профильная
- Номер вопроса в билете: 7
- Баллы: 1
- Сложность: Базовый
-
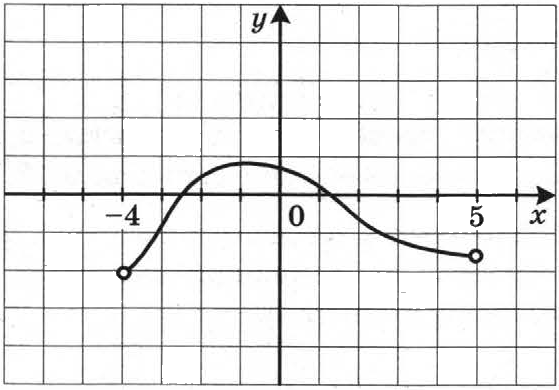
На рисунке изображён график производной функции у = f(х), определенной на промежутке (-4; 5). Найдите количество точек экстремума функции у = f(х).
 Баллы: 0
Баллы: 0 - Подробное решение
На графике не функция, а производная функции.
Точки в которых производная функции обращается в ноль - это и есть точки экстремума функции. (точки локального максимума или минимума) Точки где у обращается в ноль на графике очень хорошо видно. Это точки где график пересекает ось Ox. Таких точек у нас 2 штуки. Ответ: 2
А что еще можно сказать?
Первая точка x= −2,5 y=0 это точка локального минимума. Почему? Производная была отрицательной, функция убывала, а потом производная стала положительной функция стала возрастать. Смена убывания на возрастание означает, что это точка локального минимума.
Вторая точка x= 1,2 y=0 это точка локального максимума. Почему? Производная была больше нуля, функция возрастала, а потом производная стала меньше нуля функция стала убывать. Смена возрастания на убывание означает, что это точка локального максимума.
Помоги нам - задонать!