- Дисциплина: Математика профильная
- Номер вопроса в билете: 7
- Баллы: 1
- Сложность: Базовый
-
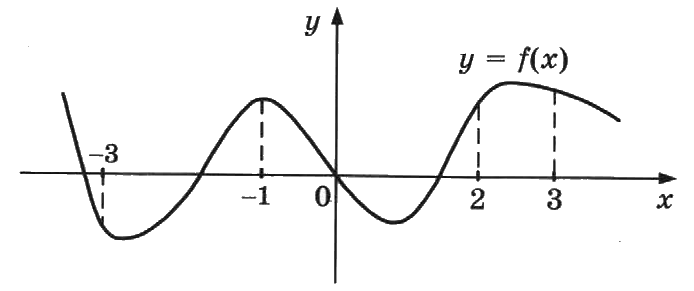
На рисунке изображён график функции у = f(x) и отмечены точки -3, -1, 2, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
 Баллы: 0
Баллы: 0 - Подробное решение
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох.
в точке с абсциссой x=−3 функция убывает, производная будет отрицательной;
в точке с абсциссой x=−1 функция имеет локальный максимум, производная будет равна нулю;
в точке с абсциссой x=2 функция возрастает, производная будет положительной;
в точке с абсциссой x=3 функция убывает, производная будет отрицательной.
Итак у нас есть 2 отрицательных производных. Какая из них меньше? Та, где функция сильнее убывает, там где график убывания круче. В точке с абсциссой x=−3 график куда круче идёт вниз чем в точке с абсциссой x=3. Можно ещё построить касательные из эти точек. Чем меньше тупой угол угол между касательной и осью Ox, тем тангенс тупого угла меньше. (Чем ближе тупой угол к 90 градусам)
Ответ −3
А если из двух положительных производных по графику функции надо найти наибольшую, то как быть? Аналогично. Чем круче функция возрастает, тем больше производная. Чем ближе острый угол образованный касательной проведенной через точку к оси oX, к 90 градусам, тем тангенс этого угла больше.
Помоги нам - задонать!