- Дисциплина: Математика базовая
- Номер вопроса в билете: 16
- Баллы: 1
- Сложность: Базовый
-
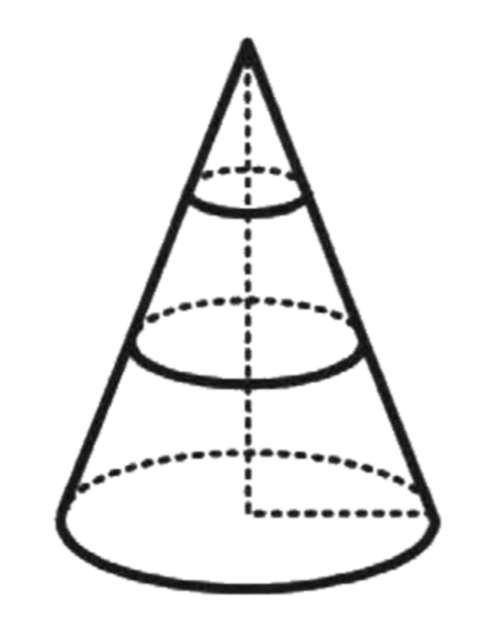
В конусе проведено два сечения плоскостями, параллельными плоскости основания конуса. Точками пересечения данных плоскостей с высотой конуса высота делится на 3 равных отрезка. Найдите объём средней части конуса, если объём нижней части равен 38.
 Баллы: 0
Баллы: 0 - Подробное решение
Пусть R1- радиус верхнего сечения, а R2- радиус нижнего сечения
Воспользуемся формулой нахождения объема усеченного конуса:
R-радиус верхней части
2R- радиус средней части
3R-радиус нижней части
Ответ: 14
Сайт помог тебе решить задачу?
Помоги нам - задонать!
Помоги нам - задонать!