- Дисциплина: Математика базовая
- Номер вопроса в билете: 15
- Баллы: 1
- Сложность: Базовый
-
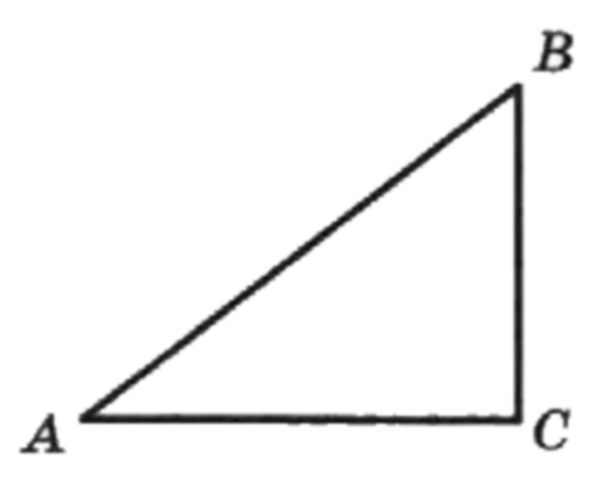
В прямоугольном треугольнике АВС с прямым углом С
Найдите .
 Баллы: 0
Баллы: 0 - Подробное решение
Следовательно:
Найдем ВС по теореме Пифагора:
Ответ: 3
Сайт помог тебе решить задачу?
Помоги нам - задонать!
Помоги нам - задонать!