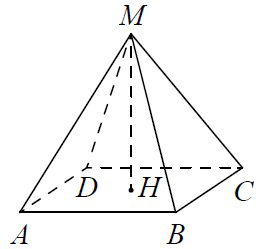
В основании правильной четырехугольной пирамиды находится квадрат.

 $S_{осн}=S_{ABCD}=4^2=16$ 

Высота правильной четырехугольной пирамиды перпендикулярна основанию и попадает в его центр. Рассмотрим прямоугольный треугольник AHM. В нем MH – высота пирамиды, AM – боковое ребро пирамиды, AH – половина диагонали основания пирамиды.

 $\displaystyle{ h=МН=\sqrt {АМ^2-({1 \over 2}AC)^2 } }$ 

но тут нам для расчетов требуется знать AC

Найдем AC - AC - это диагональ квадрата, или гипотинуза в прямоугольном треугольнике ABC, где два катета AB и BC равны 4.

 $AC = \sqrt{AB^2 + BC^2}+ \sqrt{4^2 + 4^2}=\sqrt{32}$ 

возвращаемся к формуле

 $\displaystyle{ h=МН=\sqrt {АМ^2- \left({1 \over 2}AC\right)^2 }=\sqrt {\sqrt{17}^2-\left( {\frac{1}{2} }\sqrt{32} \right)^2 }}$ 

 $\displaystyle{ h= \sqrt { 17 - {\frac{1}{2^2} }32 } = \sqrt { 17 - 8 }=3}$ 

 $\displaystyle{ V_ {MABCD}= {1 \over 3}\cdot S_{осн}\cdot h }$

 $\displaystyle{ V_ {MABCD}= {1 \over 3} \cdot AB^2\cdot h = {1 \over 3} \cdot 4^2\cdot 3=16}$